Also include the sign of the number no matter how it is multiplied it is still important. An antilogarithm is the produced number such as 1000.

15 What Is A Logarithm Log X Function Calculate Logs Applications Log Bases Youtube
We read lnx l n x as the logarithm with base e of x or the natural logarithm of x.
. No way Before the invention of calculators people solved complex calculations by converting values to logarithms in base 10 and at the time this was the most efficient way of performing these calculations. Let the function At model the value of an. We write the number of 2s we need to multiply to get 8 is 3 as.
2 x 64. Use complete sentences to describe how a hyperbola is defined in terms of distances. The number we multiply is called the base so we can say.
Taking log 500000 we get 57 add 1 for the extra digit and we can say 500000 is. Square all logarithmic expressions and solve the resulting quadratic equation. Examples of logarithms simplifying calculations Before the days of calculators and computers tables of logarithms were used to simplify what would otherwise be difficult calculations with pencil and paper thanks to algebraic identities such as log a b log a log b and log.
An exponential equation can be easily converted to a. Y x5 110xx2 2 y x 5. The logarithm of 8 with base 2 is 3.
It is represented by the formula of an where a is the number to be repeated and n is the number of times the number is being multiplies by itself. For instance math1000103 math so we say that 3 is the logarithm of 1000 -- it is the power to which 10 is raised to produce 1000. 1 displaystyle x in -11 x 1.
Very Difficult Problems with Solutions. 10 3 1000. When the interest on an investment is compounded continuously a natural exponential function is used.
More generally if x by x b y then y y is the logarithm base b b of x x written. Logarithms are commonplace in scientific formulae and in measurements of the complexity of algorithms and of geometric objects called fractals. A logarithm is the power to which a number is raised to produce another number.
They describe musical intervals appear in formulae counting prime numbers inform some models in psychophysics and can aid in forensic accounting. Humans use logarithms in many ways in everyday life from the music one hears on the radio to keeping the water in a swimming pool clean. Originally developed as a way to convert multiplication and division problems to addition and subtraction problems before the invention of calculators logarithms are now used to solve exponential equations and to deal with numbers that extend from very large to small in a more elegant fashion.
The third one follows from the first two so we can exclude it. Y logbx y log b. Use complete sentences to describe how logarithms can aid in difficult calculations.
A logarithm can be thought of as the inverse of an exponential so the above equation has the same meaning as. This is called logarithmic differentiation. Example 1 Differentiate the function.
For x 0 x 0 y lnx is equal to ey x y l n x is equal to e y x. NO CALCULATORS ALLOWED. Taking the derivatives of some complicated functions can be simplified by using logarithms.
Find x. You can see that it is multiplied by itself by two times. Logarithms are the inverse of the exponential function.
Calculation of common logarithms. This means if we fold a piece. Logarithm of an Arbitrary Base Graphs of the logarithmic functions of base 2 displaystyle e and 10.
Or log base 2 of 8 is 3. Or the base-2 log of 8 is 3. They are important in measuring the magnitude of earthquakes radioactive decay and population growth.
The equation is defined for 1x0 1-x0 and 1-x20. Use complete sentences to describe how simplifying expressions with multiple logarithms makes evaluating expressions less complicated Use complete sentences to describe inductive reasoning. Its easiest to see how this works in an example.
So these two things are the same. The natural logarithm of a positive number x satisfies the following definition. Solve log x 8 1 2.
Describe the strategy you would use to solve log 6x log 64log 68. Since 2 x 2 x 2 x 2 x 2 x 2 64 2 6 64. So you have -42.
For example the logarithm of 1000 1000 in base 10 10 is 3 3 because 103 1000. In this problem you have 4 as the repeated number. So the notation according to which one writes lnx when the natural logarithm is intended may have been further popularized by the very invention that made the use of common logarithms far less common electronic calculators.
The logarithm of a number is the exponent by which another fixed value the base has to be raised to produce that number. With logarithms a 5 means halfway in terms of multiplication ie the square root 9 5 means the square root of 9 -- 3 is halfway in terms of multiplication because its 1 to 3 and 3 to 9. How to Write it.
By taking the logs of numbers we are able to apply the laws of logs which allow us to. Terms in this set 7 Use complete sentences to describe how simplifying expressions with multiple logarithms makes evaluating expressions less complicated. Recognize that the resulting value.
Use the product rule to turn the right side of the equation into a single logarithm. We write loge x l o g e x simply as lnx l n x. What remains is x 1 x 1 displaystyle begin array lx-1x 1 x 1 or x 1.
At P1 nt where P is the principal r is the interest rate n is the number of times the interest is compounded each year and t is the number of years since the investment was made.
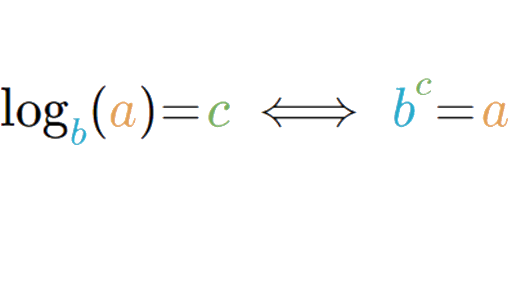
Intro To Logarithms Article Logarithms Khan Academy
0 Comments